Введение.
Издавна человек стремился окружить себя
красивыми вещами. На первый взгляд, красота не
имеет важного значения для жизни человека. Но
с доисторических времен люди старались сделать
красивыми даже обычные предметы обихода.
Люди не только создавали красивые предметы,
но и любовались ими и задавались вопросом: почему этот предмет красив, он нравится, а другой,
очень похожий, не нравится.
Тогда из творцов
они превращались в исследователей красоты.
Ведь красота скульптуры, храма, картины различна, но есть между ними что-то общее. Красота
и гармония стали важнейшими категориями познания. В своих творениях люди чаще используют
правильные геометрические формы – квадрат,
круг, равнобедренный треугольник, пирамиду.
В пропорциях различных сооружений предпочтительны целочисленные соотношения. Но часто
при создании гармонических произведений человек пользовался и издавна известной Золотой
пропорцией, которая получается при золотом
рассечении отрезка.
Золотое сечение (ЗС) – это сечение, которое
делит отрезок на две неравные части, когда от-
ношение меньшей части к большей равно отношению большей части к длине всего отрезка. Значение этого отношения φ = 0,6180339875… ≈ 0,62
называют золотой константой или малым коэффициентом, а обратную величину Ф = 1/φ =
= 1,6180339875… ≈ 1,62 – большим коэффициентом золотой пропорции.
При таком рассечении отрезка доли частей составляют 0,62 ≈ φ и
0,38 ≈ φ². Именно эти «золотые» числа чаще всего
проявляются в различных отраслях науки (математике, ботанике, биологии, астрономии), а также
в архитектуре и живописи в виде отношений
однородных параметров [1].
Пропорции золотого сечения в архитектуре использовалось при строительстве всех великих сооружений мира – Парфенон, Египетские пирамиды, храм Святой Софии
в Константинополе, Смольный собор в Санкт-Петербурге, Успенский собор Елецкого монастыря в Чернигове, великая Печерская церковь в
Киеве и таких примеров огромное множество.
Изучая применение золотого сечения в строительстве этих сооружений становится ясно, что использование золотого сечения в строительстве
является крайне разумным.
Пропорции золотого сечения в архитектуре еще недостаточно изучены
и относительно мало применяется. Но есть попытки конструктивного использования закономерностей ее проявления в технических науках.
Так, Коробко В.И. установил связь основных интегральных физико-механических характеристик
плоских элементов строительных конструкций
с золотой пропорцией. Используя эту связь он
на уровне изобретений разработал способы неразрушающего контроля качества строительных
конструкций [2].
Золотые сечения «Каменного моста».
Авторами проведен анализ размеров самого известного водопропускного сооружения в Томске –
«Каменного моста» на предмет наличия золотого сечения в его архитектурном облике. Этот
мост был возведен сто лет назад (в 1916 г.). Он
содержит железобетонное пролетное строение,
четыре ростральные колонны по углам, которые
украшены гирляндами и головами неведомых
существ, два обелисковых фонаря с каждой стороны и решетчатые ограждения. Мост обладает
большой пропускной способностью. Наличие золотой пропорции выявлено в соотношениях как
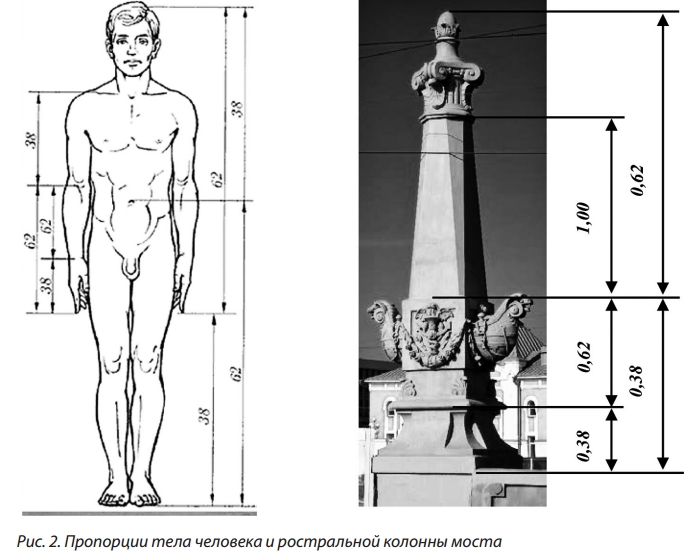
основных размеров моста (рис. 1), так и отдельных его элементов: ростральных колонн (рис. 2),
ограждений (рис. 3) и фонарных столбов (рис. 4).
Такая пропорция придает мосту гармоничный и
выразительный вид.

Золотое сечение в геометрии струи на водосливе. Можно заметить, что эмпирические коэффициенты в формулах для расчета истечения
жидкости через отверстия, насадки и водосливы
часто приобретают значения коэффициентов
золотой пропорции и их инвариантов (0,38;
0,62; 0,79). Это побудило изучить вопрос о наличии золотого сечения в геометрии потоков
жидкости [3].
На рис. 5 указаны основные вертикальные и
горизонтальные размеры струи на водосливе
прямоугольного сечения без бокового сжатия по
классическим опытам Базена (1898 г.) и по ТУиН
МЭС СССР (1951 г.) [4, 5].
Проведенный анализ показывает, что все отношения основных размеров струи являются
членами одной геометрической прогрессии со
знаменателем φ1/6.
В этом случае отношение любых размеров струи Аi и А, в т.ч. и приведенные
на рис. 5 коэффициенты пропорциональности
при Н, совпадают с погрешностью менее 0,64%
с членами ряда
Аi / А = φ±k/6, (1)
где: k = 0, 1, 2, 3, …; при Аi < А принимается «+»,
иначе – «–».
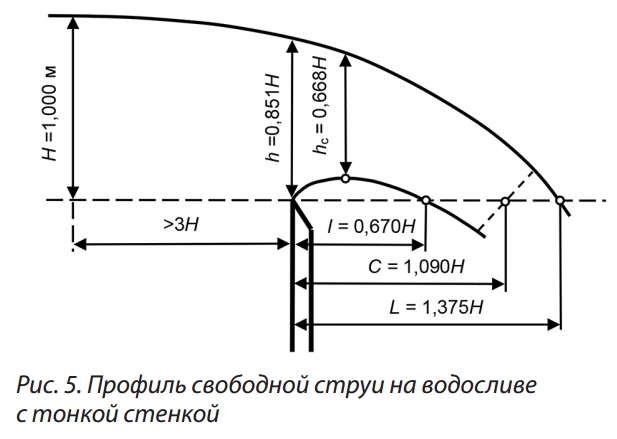
Так, например, h/L = 0,851/1,375 = 0,6189… ≈
≈ φ = φ6/6. Можно также показать, что сжатое сечение струи с размером hс с достаточно высокой
точностью делит отрезок l в золотой пропорции
(сжатое сечение струи является золотым сечением для отрезка l). Таким образом, показано, что
форма свободной струи на водосливе с тонкой
стенкой соответствует принципу золотого сечения.
Известно, что по форме нижней поверхности
этой струи создан водослив практического профиля (Кригера-Офицерова) с криволинейным
очертанием, который, по сравнению с другими
типами водосливов, обладает повышенной пропускной способностью. Причем его коэффициент
расхода определяется по эмпирической формуле
Розанова: m = 0,504 [0,62 + 0,38(H/H*)1/3]. Здесь H и
H* действительный и расчетный напор. Следует
заметить, что формула содержит сразу две золотые константы, дополнительно подтверждающие
наличие золотого сечения в форме такого водослива.
Предельные коэффициенты сжатия струи.
Коэффициенты сжатия представляют собой отношение линейных размеров, например, диаметров
(ε = dс / d – диаметр сжатого сечения струи/диаметр отверстия) или площадей: (εω= ωс /ω – площадь сжатого сечения струи/площадь отверстия).
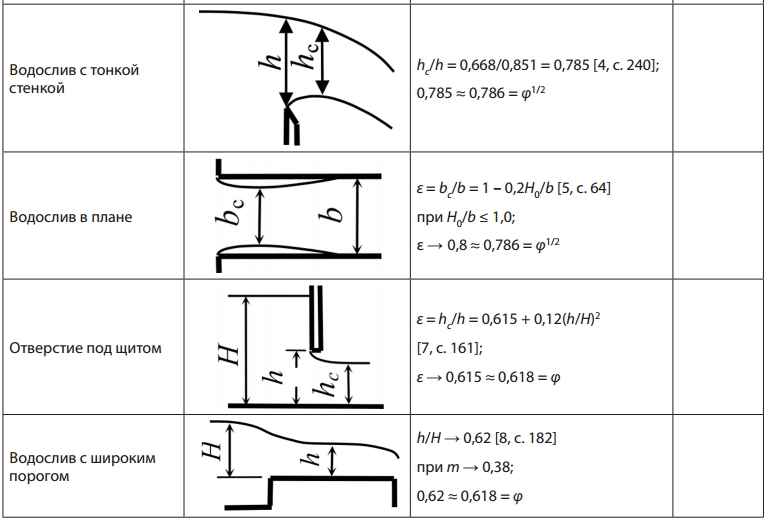
В табл. 1 представлены эмпирические формулы
для коэффициентов сжатия струи и их предельные (справочные) значения при совершенном
истечении жидкости через отверстия, насадки
и водосливы.
Коэффициенты сжатия приобретают предельные (постоянные) значения, когда относительные размеры выходного сечения канала (h/H,
d/D), силы вязкости и поверхностного натяжения
малы. Например, при истечении различных жидкостей через малые отверстия c острой кромкой,
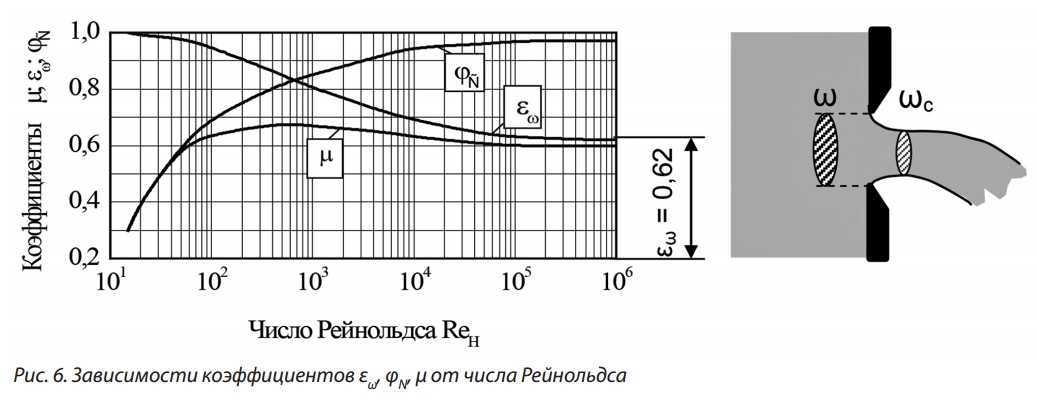
значение коэффициента сжатия при числах Рейнольдса Re > 105 и Вебера We > 200 стабилизируется и становится близким к рекомендуемому
для расчетов: εω
= 0,62 ≈ φ (рис. 6). На такое же
предельное значение указывает и эмпирическая
формула для εω при истечении из цилиндрического резервуара диаметром D через круглое
отверстие диаметром d, расположенное на его
оси, при больших значениях Re (табл. 1). В этой
формуле представлены сразу два золотых числа:
0,62 и 0,38. Из формулы видно, что при уменьшении относительного размера отверстия d/D, когда
влияние стенок сосуда (резервуара) на истечение
уменьшается и сжатие струи становится совершенным, второе слагаемое стремится к нулю, а
коэффициент сжатия приобретает предельное
значение εω
= 0,62, равное золотой константе φ.
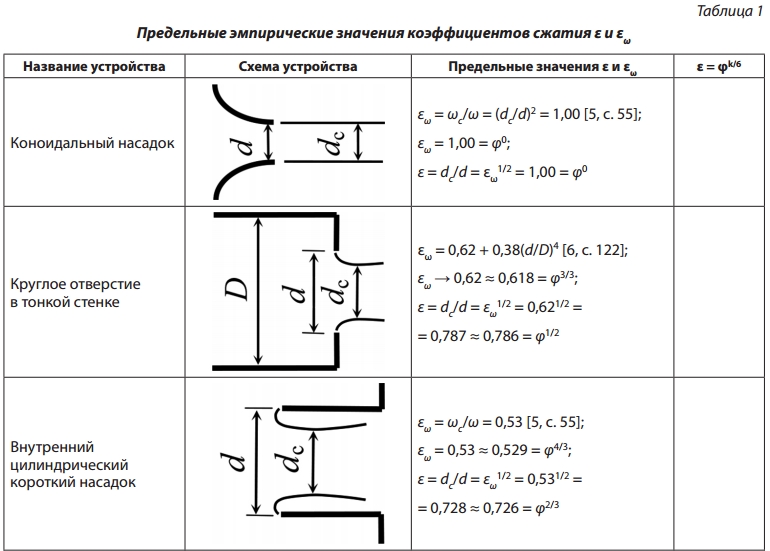
Из табл. 1 видно, что предельные коэффициенты сжатия по линейному размеру ε находятся
в соответствии с формулой (1). При изменении
геометрии (типа) водопропускного устройства
эти коэффициенты изменяются ступенчато (квантованно) и приобретают дискретные значения,
определяемые общей для отверстий, насадков
и водосливов формулой через константу
φ:
ε = φk/6, (2)
где: k = 0, 1, 2, 3, …
Тогда, при истечении через каналы круглого
сечения предельные коэффициенты сжатия струи
по площади ε
ω должны совпадать с рядом следу-
ющих инвариантов золотых чисел:
εω
= ωс / ω = (dс / d)2 = ε2 = (φk/6)2 = φk/3 ≈
≈ 1,00 – 0,85 – 0,73 – 0,62 – 0,53, (3)
что подтверждается опытными данными (табл. 1).
Следует заметить, что коноидальный насадок,
выполненный по форме свободной струи с коэффициентом сжатия εω
= ωс / ω = 0,62 = φ, обладает
наибольшей пропускной способностью по сравнению с другими типами насадков.
ВЫВОДЫ
1. Водопропускные сооружения, спроектированные с учетом принципа золотого сечения,
приобретают гармоничный и выразительный вид.
2. Установлено, что геометрия свободных
струй при развитом истечении через отверстия, насадки и водосливы подчиняется
золотой пропорции, а ее учет при создании
устройств и сооружений обеспечивает им
более высокую пропускную способность.
3. Работа призвана обратить внимание специалистов в области гидравлики и гидротехники на феноменологические свойства золотой
пропорции и на методологию возможного
научного подхода при обобщении результатов экспериментальных исследований и
при поиске оптимальных технических решений водопропускных устройств и сооружений.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Коробко В.И. Золотая пропорция и проблемы
гармонии систем. – М.: Изд-во Ассоциации строительных вузов стран СНГ, 1998. – 373 с.
2. Балакшин О.Б. Коды да Винчи – новая роль в
естествознании? Неожиданное о золотом сечении:
Гармония асимметричных подобий в природе. – М.:
КомКнига, 2005. – 112 с.
3. Слабожанин Г.Д. Сводные таблицы предельных
параметров истечения жидкости через отверстия, насадки и водосливы // Гидротехнические сооружения. –
2009. – № 6. – С. 97–103.
4. Агроскин И.И., Дмитриев Г.Т., Пикалов Ф.И.
Гидравлика: Учебник для вузов / Под ред. И.И. Агроскина. – М.; Л.: Энергия, 1964. – С. 240.
5. Справочник по гидравлическим расчетам / Под
ред. П.Г. Киселева. – М.: Энергия, 1974. – С. 61.
6. Бутаев Д.А., Калмыкова З.А., Подвидз Л.Г. и др.
Сборник задач по машиностроительной гидравлике:
Учеб. пособие для машиностроительных вузов / Под
ред. И.И. Куколевского, Л.Г. Подвидза. – М.: Изд-во
МГТУ, 2002. – С. 121.
7. Курганов А.М., Федоров Н.Ф. Гидравлические
расчеты систем водоснабжения и водоотведения:
Справочник / Под ред. А.М. Курганова. – Л.: Стройиздат, 1986. – С. 161.
8. Константинов Ю.М. Гидравлика: Учебник. – К.:
Вища шк., 1988. – С. 182.



